GAMES101 Lecture09 Shading 3
Lecture_09_Shading 3 (Texture Mapping cont.)
Barycentric coordinates(重心坐标)#
为什么插值?
- 指定顶点上的值
- 获得三角形内平滑变化的值
可以插值什么内容?
- Texture coordinates(纹理坐标), colors(颜色), normal vectors(法线),…
重心坐标公式#
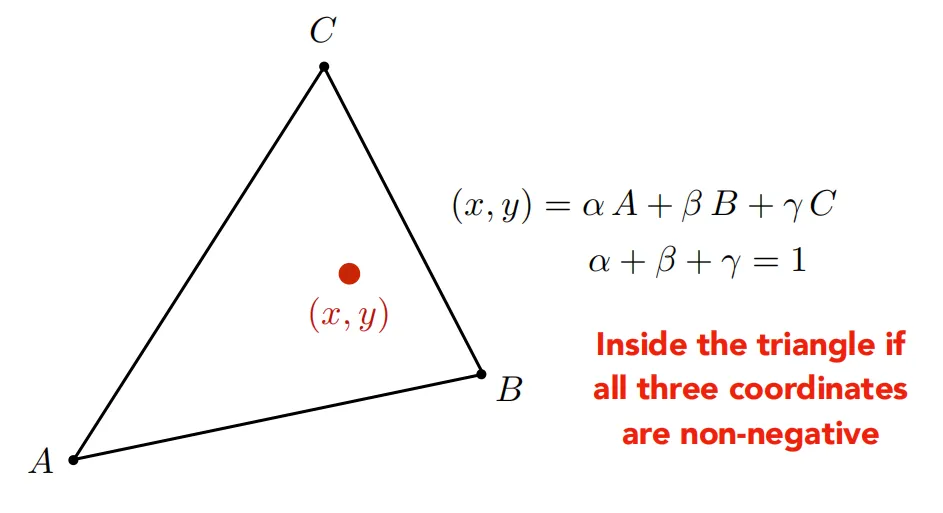
由可求得:
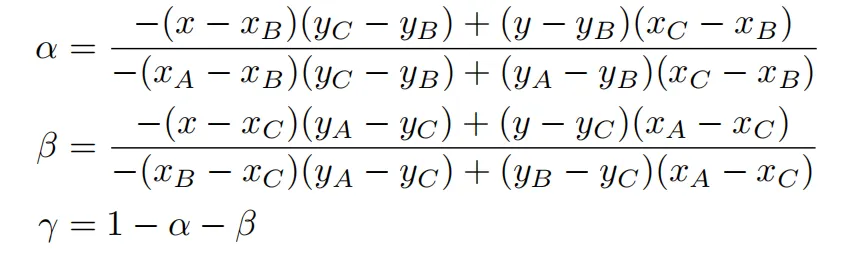
注意:重心坐标在投影下是会变化的。
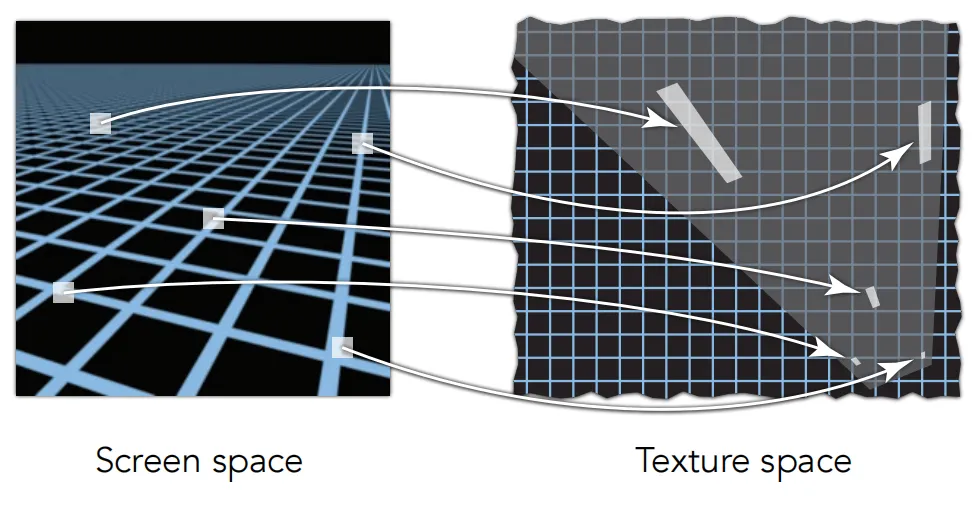
Applying Textures(应用纹理)#
我们要将纹理应用到物体上。(x,y)是像素坐标,(u,v)是纹理坐标。
纹理应用步骤:
对于每一个光栅化的屏幕像素: (u,v) = 计算(x,y)处对应的纹理坐标 (x,y)是使用的重心坐标
texcolor(纹理颜色) = texture.sample(u,v); 纹理上取样纹理坐标(u,v)处的颜色
将样本颜色设置为texcolor; 通常会使用Blinn-Phong reflectance model
Texture Magnification 纹理放大#
Easy Case(纹理太小)#
这意味着多个个像素需要对应同一个texel(纹理元素,纹素,即在纹理上的一个像素)
我们可以使用Bilinear Interpolation(双线性插值,考虑周围2x2邻域)和Bicubic Interpolation(双三次插值,考虑周围4x4邻域)来解决这个问题。
下面介绍的是Bilinear Interpolation(双线性插值法):
如何取样纹理上(u,v)处的值f(x,y)?
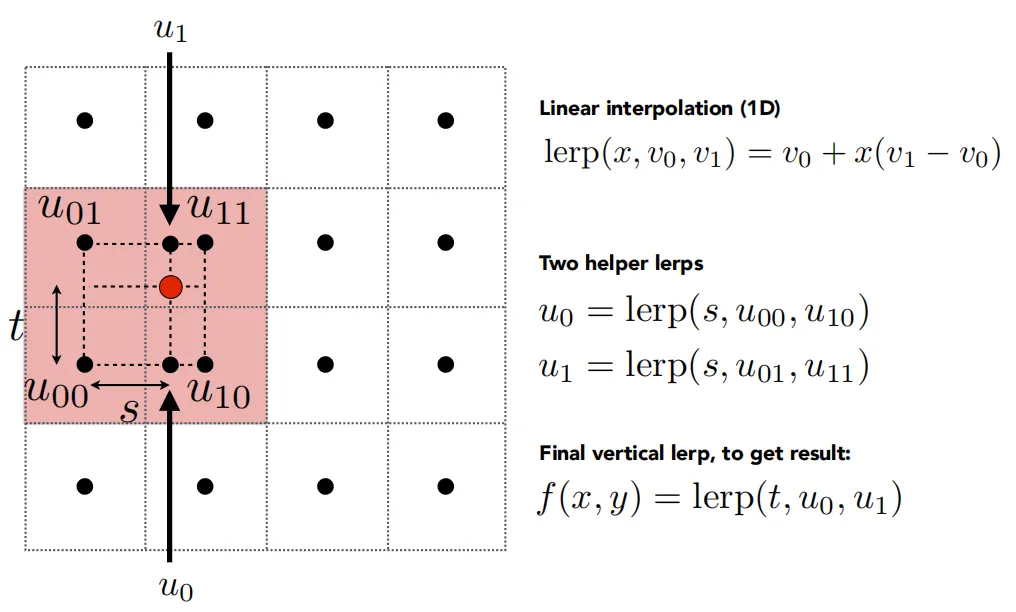
先进行水平插值,求出和,再进行垂直插值求出
处理效果:

Hard case(纹理太大)#
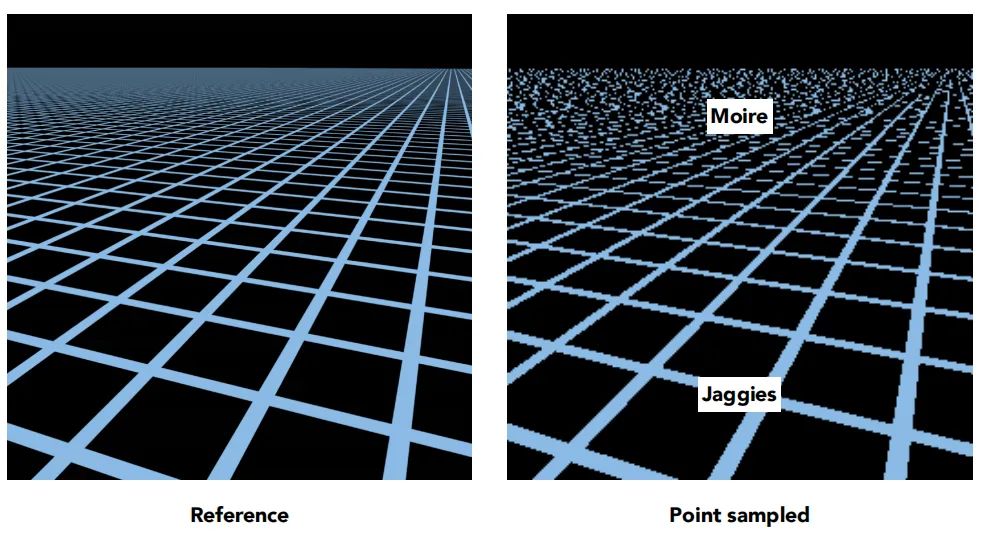
如果我们还是使用点插值,将会出现多个纹理元素只对应一个像素的问题,即采样率过低,这种现象被称为Texel Footprint。
在图像上,便体现为出现Moire(摩尔纹)和Jaggies(锯齿)。
Super sampling(超采样)将会解决问题,但是太过于耗费计算资源,如何解决?可以在不同的位置采取不同的采样率!
Mipmap#
可以允许快速查询某个范围的近似值,但是注意只能方形!

每次都将的像素合成为1个新像素,例如图中的图像共有8层。
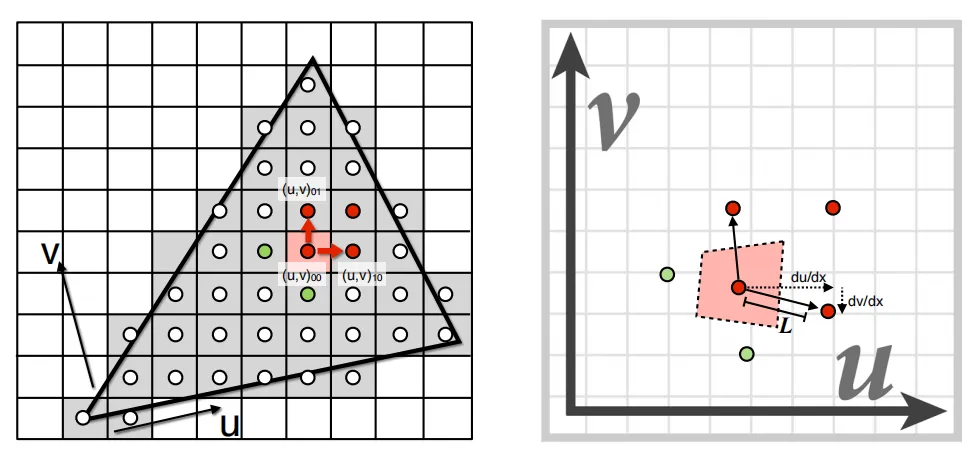
Compluting Mipmap Level D(计算层级)#
使用相邻的屏幕纹理来计算Texture Footprint。
-
:表示沿屏幕 x方向(水平)纹理的拉伸程度。
-
:表示沿屏幕 y 方向(垂直)纹理的拉伸程度。
-
L:取两者的最大值,即纹理在像素空间中的最大拉伸比例。
-
:将拉伸比例 L转换为对数尺度,对应Mipmap的层级。
- 若 L=1(纹理与像素1:1映射),则 D=0,使用原始纹理(Level 0)。
- 若 L=4(纹理被拉伸4倍),则 D=2,选择Level 2的Mipmap(缩小4倍的纹理)。
- 若 L<1(纹理被压缩),可能启用各向异性过滤或更高分辨率层级。
mipmap计算层级效果如下图,不同距离采样率不同:
 但我们会发现边界处无渐变处理,可以使用基于D值的线性插值使Mipmap Level变化平滑。
但我们会发现边界处无渐变处理,可以使用基于D值的线性插值使Mipmap Level变化平滑。
效果如图:

Anisotropic Filtering(各向异性过滤)#
如果Pixel Footerprint不是方形而是不规则图形,那么mipmap的效果不太好,需要使用各项异性过滤解决。
Mipmap得到的一系列的纹理图其实就是对角线上的卫星,可以看到都是正方形的,而各向异性过滤会对把原纹理图缩放成不同大小的矩形,各向异性生成的一系列纹理图也叫Ripmaps。
每一行是对纹理图做宽度压缩,每一列是对纹理图做高度压缩。

但非常不规则的图形仍然无法用各向异性过滤来解决,需要使用EWA Filtering方法。
使用椭圆形去近似不规则图形,然后多次查询得到加权平均值,但耗时长。
